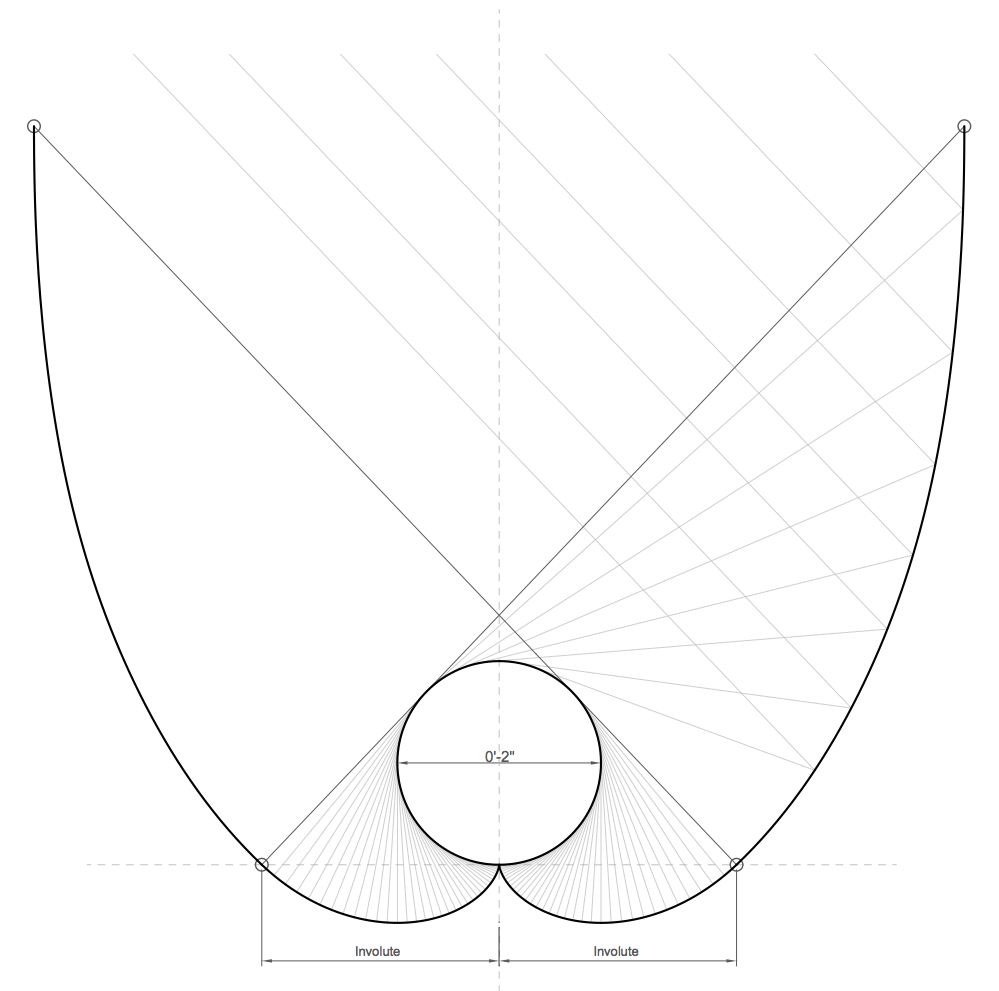

The shape of this trough has a special property: regardless of the angle at which light enters, the light is reflected into the same circular target area. When the target area corresponds with the vacuum collection tube, this means that the vast majority of the light falling into the trough is collected by the vacuum tube as useable heat. These troughs, when properly constructed, will multiply the output of a vacuum collection tube by 3.5 to 4 times. Since the trough collects light regardless of how it enters, that means this is effectively a stationary tracking system. Systems based on parabolas require precise motors to perform constant realignments, as being off by a few degrees means most of the energy will be lost; this system works with no motion at all, regardless of the season and the sun's position in the sky.
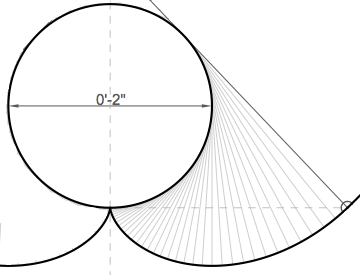
The most important part of the trough is the bottom, everything from the vacuum collection tube down. Each of the two lowest points in the trough are involutes of the shape of the collector. You can think of an involute as being the target shape, unwound. It's actually easy to draw your own perfect involute shape; all you need is something round that's the same size as your collector, a string, and a pencil. Tie a small loop in the end of the string; the tip of the pencil will go in this loop. Wrap the string around the shape you're creating the involute of, making sure that the tip of the pencil is at the bottom of the shape, and hold the other end of the string tight, pressing against the shape. Pull the pencil down and away from the shape. As you do, keep the string tight at all times. The line will start out going almost straight down, curve sharply around the bottom, and then begin a graceful and progressively more relaxed curve back up. (to see some simple animations of this being done, look up "involute" on Wikipedia)
To understand why this shape works to collect light as it does, first think of a simple mirror. Pick a point somewhere on this mirror, and then extend an imaginary line straight up from the surface of the mirror from that point. This line is called the "normal", and it's exactly perpendicular to the mirror. If you shine a light on your selected point from some angle, the light will reflect off the mirror, on the other side of the normal, at the same angle it came in on.
Now, curve the mirror; bend it unto a U shape. Before, there was only one normal for the entire mirror; now, every point has a different normal. But, the rules of reflection apply to a curved surface as they do for a flat surface; the only difference is that for a curved surface, every point reflects light in a slightly different direction (since every point has a different normal).
Back to the involute. The magic of the involute is that, for every point along it, the normal of that point is tangent to the target circle. Being a tangent means that the line of the normal just touches the edge of the circle, at exactly one point (but doesn't cut through the circle, and doesn't miss it entirely). If you think about this in terms of reflections, it means that for every point on the involute, if light is shining from one side of the normal, it never actually hits that point -- it hits the target circle first. And if light is shining from the other side of the normal, then it's reflected back up into the target.